This post is completed by 4 users

  • 1
 Add to List
Beginner

270. Weighted Graph Implementation – JAVA

We have already discussed about Graph basics. We recommend reading this before you continue to read this article.

What is Weighted Graph?

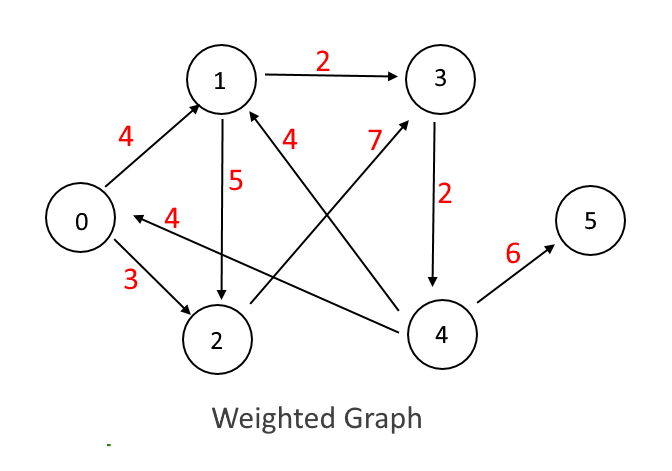
A Graph is called weighted graph when it has weighted edges which means there are some cost associated with each edge in graph.

Example:

Implementation:

  1. Each edge of a graph has an associated numerical value, called a weight.
  2. Usually, the edge weights are nonnegative integers.
  3. Weighted graphs may be either directed or undirected.
  4. The weight of an edge is often referred to as the "cost" of the edge.
  5. Will create an Edge class to put weight on each edge




import java.util.LinkedList;

public class Main {
    static class Edge {
        int source;
        int destination;
        int weight;

        public Edge(int source, int destination, int weight) {
            this.source = source;
            this.destination = destination;
            this.weight = weight;
        }
    }

    static class Graph {
        int vertices;
        LinkedList<Edge> [] adjacencylist;

        Graph(int vertices) {
            this.vertices = vertices;
            adjacencylist = new LinkedList[vertices];
            //initialize adjacency lists for all the vertices
            for (int i = 0; i <vertices ; i++) {
                adjacencylist[i] = new LinkedList<>();
            }
        }

        public void addEgde(int source, int destination, int weight) {
            Edge edge = new Edge(source, destination, weight);
            adjacencylist[source].addFirst(edge); //for directed graph
        }

        public void printGraph(){
            for (int i = 0; i <vertices ; i++) {
                LinkedList<Edge> list = adjacencylist[i];
                for (int j = 0; j <list.size() ; j++) {
                    System.out.println("vertex-" + i + " is connected to " +
                            list.get(j).destination + " with weight " +  list.get(j).weight);
                }
            }
        }
    }
      public static void main(String[] args) {
            int vertices = 6;
            Graph graph = new Graph(vertices);
            graph.addEgde(0, 1, 4);
            graph.addEgde(0, 2, 3);
            graph.addEgde(1, 3, 2);
            graph.addEgde(1, 2, 5);
            graph.addEgde(2, 3, 7);
            graph.addEgde(3, 4, 2);
            graph.addEgde(4, 0, 4);
            graph.addEgde(4, 1, 4);
            graph.addEgde(4, 5, 6);
            graph.printGraph();
        }
}



class Edge:
    def __init__(self, source, destination, weight):
        self.source = source
        self.destination = destination
        self.weight = weight

class LinkedList:
    def __init__(self):
        self.head = None

    def add_first(self, edge):
        edge.next = self.head
        self.head = edge

class Graph:
    def __init__(self, vertices):
        self.vertices = vertices
        self.adjacency_list = [LinkedList() for _ in range(vertices)]

    def add_edge(self, source, destination, weight):
        edge = Edge(source, destination, weight)
        self.adjacency_list[source].add_first(edge)

    def print_graph(self):
        for i in range(self.vertices):
            current = self.adjacency_list[i].head
            while current:
                print(f"vertex-{i} is connected to {current.destination} with weight {current.weight}")
                current = current.next

if __name__ == "__main__":
    vertices = 6
    graph = Graph(vertices)
    graph.add_edge(0, 1, 4)
    graph.add_edge(0, 2, 3)
    graph.add_edge(1, 3, 2)
    graph.add_edge(1, 2, 5)
    graph.add_edge(2, 3, 7)
    graph.add_edge(3, 4, 2)
    graph.add_edge(4, 0, 4)
    graph.add_edge(4, 1, 4)
    graph.add_edge(4, 5, 6)

    graph.print_graph()



package main

import "fmt"

type Edge struct {
	destination int
	weight      int
	next        *Edge
}

type Graph struct {
	vertices      int
	adjacencyList []*Edge
}

func newGraph(vertices int) *Graph {
	adjacencyList := make([]*Edge, vertices)
	return &Graph{vertices, adjacencyList}
}

func (g *Graph) addEdge(source, destination, weight int) {
	edge := &Edge{destination, weight, nil}
	edge.next = g.adjacencyList[source]
	g.adjacencyList[source] = edge
}

func (g *Graph) printGraph() {
	for i := 0; i < g.vertices; i++ {
		current := g.adjacencyList[i]
		for current != nil {
			fmt.Printf("vertex-%d is connected to %d with weight %d", i, current.destination, current.weight)
			fmt.Println("")
			current = current.next
		}
	}
}

func main() {
	vertices := 6
	graph := newGraph(vertices)
	graph.addEdge(0, 1, 4)
	graph.addEdge(0, 2, 3)
	graph.addEdge(1, 3, 2)
	graph.addEdge(1, 2, 5)
	graph.addEdge(2, 3, 7)
	graph.addEdge(3, 4, 2)
	graph.addEdge(4, 0, 4)
	graph.addEdge(4, 1, 4)
	graph.addEdge(4, 5, 6)

	graph.printGraph()
}

Output:

vertex-0 is connected to 2 with weight 3
vertex-0 is connected to 1 with weight 4
vertex-1 is connected to 2 with weight 5
vertex-1 is connected to 3 with weight 2
vertex-2 is connected to 3 with weight 7
vertex-3 is connected to 4 with weight 2
vertex-4 is connected to 5 with weight 6
vertex-4 is connected to 1 with weight 4
vertex-4 is connected to 0 with weight 4

Reference: here

Related Problems: